Topic modeling
The topicmod module offers a wide range of tools to facilitate topic modeling with Python. This chapter will introduce the following techniques:
parallel topic model computation for different copora and/or parameter sets
evaluation of topic models (including finding a good set of hyperparameters for the given dataset)
export of topic models and summaries to different file formats
A quick note on terminology: So far, we spoke about tokens or sometimes terms when we meant the individual elements that our documents consist of after we applied text preprocessing such as tokenization to the raw input text strings. These tokens can be lexicographically correct words, but they don’t have to, e.g. when you applied stemming you might have tokens like “argu” in your vocabulary. There may also be numbers or punctuation symbols in your vocabulary. For those topic modeling techniques that tmtoolkit supports, the results are always two probability distributions: a document-topic distribution and a topic-word distribution. Since the latter is called topic-word and not topic-token or -term distribution, we will also use the term word when we mean any token from the corpus’ vocabulary.
An example document-term matrix
tmtoolkit supports topic models that are computed from document-term matrices (DTMs). Just as in the previous chapter, we will at first generate a DTM. However, this time the sample will be bigger:
[1]:
import random
random.seed(20191120) # to make the sampling reproducible
import numpy as np
np.set_printoptions(precision=5)
from tmtoolkit.utils import enable_logging
enable_logging()
from tmtoolkit.corpus import Corpus, print_summary
corp = Corpus.from_builtin_corpus('en-NewsArticles', sample=100)
print_summary(corp)
2023-05-03 15:23:11,614:INFO:tmtoolkit:creating Corpus instance with no documents
2023-05-03 15:23:11,615:INFO:tmtoolkit:using serial processing
2023-05-03 15:23:11,832:INFO:tmtoolkit:sampling 100 documents(s) out of 3824
2023-05-03 15:23:11,835:INFO:tmtoolkit:adding text from 100 documents(s)
2023-05-03 15:23:11,836:INFO:tmtoolkit:running NLP pipeline on 100 documents
2023-05-03 15:23:15,164:INFO:tmtoolkit:generating document texts
Corpus with 100 documents in English
> NewsArticles-1137 (226 tokens): These Cool New ' Vertical Forest ' Skyscrapers Are...
> NewsArticles-1141 (914 tokens): Aslef members reject Southern rail deal Aslef m...
> NewsArticles-1090 (1291 tokens): Martin challenges Fitzgerald over Tusla informatio...
> NewsArticles-1032 (653 tokens): Germany 's right - wing AfD seeks to expel state l...
> NewsArticles-1048 (476 tokens): Espirito Santo police return to work after murder ...
> NewsArticles-113 (1071 tokens): Use talk not tech to tame your children 's online ...
> NewsArticles-104 (31 tokens): Your pictures : Broken resolutions Each week , ...
> NewsArticles-1126 (163 tokens): This Makeup Palette Has A Game - Changing Little S...
> NewsArticles-1043 (270 tokens): Burhan Ozbilici wins 2017 World Press Photo compet...
> NewsArticles-1036 (835 tokens): Amnesty accuses Tunisian authorities of torture ah...
(and 90 more documents)
total number of tokens: 66637 / vocabulary size: 9469
We will also now generate two DTMs, because we later want to show how you can compute topic models for two different DTMs in parallel. At first, we to some general preprocessing.
[2]:
from tmtoolkit.corpus import lemmatize, to_lowercase, remove_punctuation
lemmatize(corp)
to_lowercase(corp)
remove_punctuation(corp)
print_summary(corp)
2023-05-03 15:23:15,188:INFO:tmtoolkit:replacing 2186 token hashes
2023-05-03 15:23:15,205:INFO:tmtoolkit:replacing 502 token hashes
2023-05-03 15:23:15,211:INFO:tmtoolkit:generating document texts
Corpus with 100 documents in English
> NewsArticles-1137 (226 tokens): these cool new vertical forest skyscraper be des...
> NewsArticles-1141 (914 tokens): aslef member reject southern rail deal aslef memb...
> NewsArticles-1090 (1291 tokens): martin challenge fitzgerald over tusla information...
> NewsArticles-1032 (653 tokens): germany s right wing afd seek to expel state lead...
> NewsArticles-1048 (476 tokens): espirito santo police return to work after murder ...
> NewsArticles-113 (1071 tokens): use talk not tech to tame your child s online habi...
> NewsArticles-104 (31 tokens): your picture break resolution each week we publ...
> NewsArticles-1126 (163 tokens): this makeup palette have a game change little sec...
> NewsArticles-1043 (270 tokens): burhan ozbilici win 2017 world press photo competi...
> NewsArticles-1036 (835 tokens): amnesty accuse tunisian authority of torture ahead...
(and 90 more documents)
total number of tokens: 66637 / vocabulary size: 6758
Check if there are a few odd, unprintable characters in any tokens:
[3]:
import string
from tmtoolkit.corpus import corpus_unique_chars
{(c, c.encode('utf-8')) for c in corpus_unique_chars(corp) if c not in string.printable}
[3]:
{('\xa0', b'\xc2\xa0'),
('à', b'\xc3\xa0'),
('ó', b'\xc3\xb3'),
('™', b'\xe2\x84\xa2'),
('�', b'\xef\xbf\xbd')}
Remove all of them but “à” and “ó”
[4]:
from tmtoolkit.corpus import remove_chars
unprintable_bytes = {b'\xc2\xa0', b'\xe2\x84\xa2', b'\xef\xbf\xbd'}
unprintable_chars = set(map(lambda b: b.decode('utf-8'), unprintable_bytes))
remove_chars(corp, unprintable_chars)
# check again
{(c, c.encode('utf-8')) for c in corpus_unique_chars(corp) if c not in string.printable}
2023-05-03 15:23:15,240:INFO:tmtoolkit:replacing 3 token hashes
[4]:
{('à', b'\xc3\xa0'), ('ó', b'\xc3\xb3')}
Now we at first apply more “relaxed” cleaning:
[5]:
from copy import copy
from tmtoolkit.corpus import filter_clean_tokens, remove_common_tokens, remove_uncommon_tokens
corp_bigger = copy(corp)
filter_clean_tokens(corp_bigger, remove_shorter_than=2)
remove_common_tokens(corp_bigger, df_threshold=0.85)
remove_uncommon_tokens(corp_bigger, df_threshold=0.05)
print_summary(corp_bigger)
2023-05-03 15:23:15,312:INFO:tmtoolkit:creating Corpus instance with no documents
2023-05-03 15:23:15,314:INFO:tmtoolkit:using serial processing
2023-05-03 15:23:15,432:INFO:tmtoolkit:filtered tokens by mask: num. tokens was 66637 and is now 30415
2023-05-03 15:23:15,507:INFO:tmtoolkit:filtered tokens by mask: num. tokens was 30415 and is now 30415
2023-05-03 15:23:15,545:INFO:tmtoolkit:filtered tokens by mask: num. tokens was 30415 and is now 16468
2023-05-03 15:23:15,557:INFO:tmtoolkit:generating document texts
Corpus with 100 documents in English
> NewsArticles-1137 (43 tokens): new design help fight world need dont china kind d...
> NewsArticles-1141 (249 tokens): member reject southern deal member reject deal sou...
> NewsArticles-1090 (264 tokens): challenge information leader claim minister justic...
> NewsArticles-1032 (158 tokens): germany right seek state leader leader germany ask...
> NewsArticles-1048 (140 tokens): police return work murder officer return work stat...
> NewsArticles-113 (259 tokens): use talk child online like parent house like happy...
> NewsArticles-104 (7 tokens): break week publish set theme week break
> NewsArticles-1126 (19 tokens): game change little product reveal feature game new...
> NewsArticles-1043 (64 tokens): win 2017 world press win 2017 world press image ru...
> NewsArticles-1036 (241 tokens): accuse authority ahead key talk germany right grou...
(and 90 more documents)
total number of tokens: 16468 / vocabulary size: 789
Another copy of corp will apply more aggressive cleaning and hence will result in a smaller vocabulary size:
[6]:
from tmtoolkit.corpus import filter_for_pos
corp_smaller = copy(corp)
filter_for_pos(corp_smaller, 'N')
filter_clean_tokens(corp_smaller, remove_shorter_than=2)
remove_common_tokens(corp_smaller, df_threshold=0.8)
remove_uncommon_tokens(corp_smaller, df_threshold=0.1)
del corp # remove original corpus
print_summary(corp_smaller)
2023-05-03 15:23:15,580:INFO:tmtoolkit:creating Corpus instance with no documents
2023-05-03 15:23:15,581:INFO:tmtoolkit:using serial processing
2023-05-03 15:23:15,630:INFO:tmtoolkit:filtered tokens by mask: num. tokens was 66637 and is now 19002
2023-05-03 15:23:15,655:INFO:tmtoolkit:filtered tokens by mask: num. tokens was 19002 and is now 18553
2023-05-03 15:23:15,682:INFO:tmtoolkit:filtered tokens by mask: num. tokens was 18553 and is now 18553
2023-05-03 15:23:15,708:INFO:tmtoolkit:filtered tokens by mask: num. tokens was 18553 and is now 5084
2023-05-03 15:23:15,714:INFO:tmtoolkit:generating document texts
Corpus with 100 documents in English
> NewsArticles-1137 (12 tokens): new world china press day area china house office ...
> NewsArticles-1141 (54 tokens): member member member member secretary decision mem...
> NewsArticles-1090 (103 tokens): information leader minister child prime time week ...
> NewsArticles-1032 (58 tokens): germany state leader leader germany state party le...
> NewsArticles-1048 (59 tokens): police work officer work state people day police o...
> NewsArticles-113 (69 tokens): child house service house service month time child...
> NewsArticles-104 (2 tokens): week week
> NewsArticles-1126 (3 tokens): product way twitter
> NewsArticles-1043 (18 tokens): world press world press world press russia year ne...
> NewsArticles-1036 (91 tokens): authority germany right group security official mi...
(and 90 more documents)
total number of tokens: 5084 / vocabulary size: 142
We will create the document labels, vocabulary arrays and DTMs for both versions now:
[7]:
from tmtoolkit.corpus import dtm
dtm_bg, doc_labels_bg, vocab_bg = dtm(corp_bigger, return_doc_labels=True, return_vocab=True)
dtm_sm, doc_labels_sm, vocab_sm = dtm(corp_smaller, return_doc_labels=True, return_vocab=True)
del corp_bigger, corp_smaller # don't need these any more
dtm_bg, dtm_sm
2023-05-03 15:23:15,723:INFO:tmtoolkit:generating sparse DTM with 100 documents and vocab size 789
2023-05-03 15:23:15,738:INFO:tmtoolkit:generating sparse DTM with 100 documents and vocab size 142
[7]:
(<100x789 sparse matrix of type '<class 'numpy.int32'>'
with 9258 stored elements in Compressed Sparse Row format>,
<100x142 sparse matrix of type '<class 'numpy.int32'>'
with 2391 stored elements in Compressed Sparse Row format>)
We now have two sparse DTMs dtm_bg (from the bigger preprocessed data) and dtm_sm (from the smaller preprocessed data), a list of document labels doc_labels that represent the rows of both DTMs and vocabulary arrays vocab_bg and vocab_sm that represent the columns of the respective DTMs. We will use this data for the remainder of the chapter.
Computing topic models in parallel
tmtoolkit allows to compute topic models in parallel, making use of all processor cores in your machine. Parallelization can be done per input DTM, per hyperparameter set and as combination of both. Hyperparameters control the number of topics and their “granularity”. We will later have a look at the role of hyperparameters and how to find an optimal combination for a given dataset with the means of topic model evaluation.
For now, we will concentrate on computing the topic models for both of our two DTMs in parallel. tmtoolkit supports three very popular packages for topic modeling, which provide the work of actually computing the model from the input matrix. They can all be accessed in separate sub-modules of the topicmod module:
topicmod.tm_lda provides an interface for the lda package
topicmod.tm_sklearn provides an interface for the scikit-learn package
topicmod.tm_gensim provides an interface for the Gensim package
Each of these sub-modules offer at least two functions that work with the respective package: compute_models_parallel for general parallel model computation and evaluate_topic_models for parallel model computation and evaluation (discussed later). For now, we want to compute two models in parallel with the lda package and hence use compute_models_parallel from
topicmod.tm_lda.
We need to provide two things for this function: First, the input matrices as a dict that maps labels to the respective DTMs. Second, hyperparameters to use for the model computations. Note that each topic modeling package has different hyperparameters and you should refer to their documentation in order to find out which hyperparameters you need to provide. For lda, we set the number of topics n_topics to 10 and the number of iterations for the Gibbs sampling process n_iter to 1000. We
always want to use the same hyperparameters, so we pass these as constant_parameters. If we wanted to create models for a whole range of parameters, e.g. for different numbers of topics, we could provide varying_parameters. We will check this out later when we evaluate topic models.
Note
For proper topic modeling, we shouldn’t just set the number of topics, but try to find it out via evaluation methods. We should also check if the algorithm converged using the provided likelihood estimations. We will do both later on, but now focus on compute_models_parallel.
[8]:
import logging
import warnings
from tmtoolkit.utils import disable_logging
from tmtoolkit.topicmod.tm_lda import compute_models_parallel
# disable tmtoolkit logging for now (too much output)
disable_logging()
# suppress the "INFO" messages and warnings from lda
logger = logging.getLogger('lda')
logger.addHandler(logging.NullHandler())
logger.propagate = False
warnings.filterwarnings('ignore')
# set data to use
dtms = {
'bigger': dtm_bg,
'smaller': dtm_sm
}
# and fixed hyperparameters
lda_params = {
'n_topics': 10,
'n_iter': 1000,
'random_state': 20191122 # to make results reproducible
}
models = compute_models_parallel(dtms, constant_parameters=lda_params)
models
[8]:
defaultdict(list,
{'smaller': [({'n_topics': 10,
'n_iter': 1000,
'random_state': 20191122},
<lda.lda.LDA at 0x7f8a54426320>)],
'bigger': [({'n_topics': 10,
'n_iter': 1000,
'random_state': 20191122},
<lda.lda.LDA at 0x7f8a544264d0>)]})
As expected, two models were created. These can be accessed via the labels that we used in the dtms dict:
[9]:
models['smaller']
[9]:
[({'n_topics': 10, 'n_iter': 1000, 'random_state': 20191122},
<lda.lda.LDA at 0x7f8a54426320>)]
We can see that for each input DTM, we get a list of 2-tuples. The first element in each tuple is a dict that represents the hyperparameters that were used to compute the model, the second element is the actual topic model (the <lda.lda.LDA ...> object). This structure looks a bit complex, but this is because it also supports varying parameters. Since we only have one fixed set of hyperparameters per DTM, we only have a list of length 1 for each DTM.
We will now access the models and print the top words per topic by using print_ldamodel_topic_words:
[10]:
from tmtoolkit.topicmod.model_io import print_ldamodel_topic_words
model_sm = models['smaller'][0][1]
print_ldamodel_topic_words(model_sm.topic_word_, vocab_sm, top_n=3)
topic_1
> #1. people (0.172328)
> #2. country (0.128215)
> #3. attack (0.062047)
topic_2
> #1. trump (0.191129)
> #2. president (0.096484)
> #3. house (0.092843)
topic_3
> #1. al (0.085470)
> #2. syria (0.078897)
> #3. force (0.063560)
topic_4
> #1. company (0.198822)
> #2. system (0.109363)
> #3. year (0.091969)
topic_5
> #1. year (0.144537)
> #2. germany (0.075351)
> #3. family (0.056902)
topic_6
> #1. election (0.096485)
> #2. party (0.096485)
> #3. minister (0.093470)
topic_7
> #1. mr (0.223614)
> #2. morning (0.131100)
> #3. day (0.080988)
topic_8
> #1. china (0.281876)
> #2. development (0.091937)
> #3. market (0.079683)
topic_9
> #1. time (0.106740)
> #2. year (0.079250)
> #3. world (0.050144)
topic_10
> #1. report (0.150105)
> #2. police (0.141145)
> #3. man (0.114265)
[11]:
model_bg = models['bigger'][0][1]
print_ldamodel_topic_words(model_bg.topic_word_, vocab_bg, top_n=3)
topic_1
> #1. election (0.042648)
> #2. party (0.042648)
> #3. minister (0.041315)
topic_2
> #1. year (0.055496)
> #2. time (0.031095)
> #3. like (0.027947)
topic_3
> #1. people (0.048456)
> #2. country (0.039056)
> #3. american (0.036163)
topic_4
> #1. china (0.072627)
> #2. company (0.054472)
> #3. market (0.037896)
topic_5
> #1. police (0.042984)
> #2. attack (0.034798)
> #3. man (0.034798)
topic_6
> #1. say (0.094018)
> #2. take (0.021636)
> #3. member (0.017476)
topic_7
> #1. say (0.136264)
> #2. report (0.044769)
> #3. mr (0.028536)
topic_8
> #1. trump (0.103879)
> #2. president (0.086073)
> #3. house (0.050460)
topic_9
> #1. new (0.063062)
> #2. germany (0.060589)
> #3. country (0.045754)
topic_10
> #1. new (0.037512)
> #2. people (0.022978)
> #3. million (0.021572)
We could also generate models from different parameters in parallel, either for a single DTM or several. In the following example we generate models for a series of four different values for the alpha parameter. The parameters n_iter and n_topics are held constant across all models.
[12]:
var_params = [{'alpha': 1/(10**x)} for x in range(1, 5)]
const_params = {
'n_iter': 500,
'n_topics': 10,
'random_state': 20191122 # to make results reproducible
}
models = compute_models_parallel(dtm_sm, # smaller DTM
varying_parameters=var_params,
constant_parameters=const_params)
models
[12]:
[({'alpha': 0.0001, 'n_iter': 500, 'n_topics': 10, 'random_state': 20191122},
<lda.lda.LDA at 0x7f8a54424040>),
({'alpha': 0.1, 'n_iter': 500, 'n_topics': 10, 'random_state': 20191122},
<lda.lda.LDA at 0x7f8a54406020>),
({'alpha': 0.001, 'n_iter': 500, 'n_topics': 10, 'random_state': 20191122},
<lda.lda.LDA at 0x7f8a54406050>),
({'alpha': 0.01, 'n_iter': 500, 'n_topics': 10, 'random_state': 20191122},
<lda.lda.LDA at 0x7f8a544061d0>)]
We could compare these models now, e.g. by investigating their topics.
A more systematic approach on comparing and evaluating topic models, also in order to find a good set of hyperparameters for a given dataset, will be presented in the next section.
Evaluation of topic models
The package tmtoolkit provides several metrics for comparing and evaluating topic models. This can be used for finding a good hyperparameter set for a given dataset, e.g. a good combination of the number of topics and concentration paramaters (often called alpha and beta in literature). For some background on hyperparameters in topic modeling, see this blog post.
For each candidate hyperparameter set, a model can be generated and evaluated in parallel. We will do this now for the “big” DTM dtm_bg. Our candidate values for the number of topics k range between 20 and 120, with steps of 10. We make the concentration parameter for a prior over the document-specific topic distributions, alpha, depending on k as 1/k:
[13]:
var_params = [{'n_topics': k, 'alpha': 1/k}
for k in range(20, 121, 10)]
var_params
[13]:
[{'n_topics': 20, 'alpha': 0.05},
{'n_topics': 30, 'alpha': 0.03333333333333333},
{'n_topics': 40, 'alpha': 0.025},
{'n_topics': 50, 'alpha': 0.02},
{'n_topics': 60, 'alpha': 0.016666666666666666},
{'n_topics': 70, 'alpha': 0.014285714285714285},
{'n_topics': 80, 'alpha': 0.0125},
{'n_topics': 90, 'alpha': 0.011111111111111112},
{'n_topics': 100, 'alpha': 0.01},
{'n_topics': 110, 'alpha': 0.00909090909090909},
{'n_topics': 120, 'alpha': 0.008333333333333333}]
The heart of the model evaluation process is the function evaluate_topic_models, which is available for all three topic modeling packages. We stick with lda and import that function from topicmod.tm_lda. It is similar to compute_models_parallel as it accepts varying and constant hyperparameters. However, it doesn’t only
compute the models in parallel, but also applies several metrics to these models in order to evaluate them. This can be controlled with the metric parameter that accepts a string or a list of strings that specify the used metric(s). These metrics refer to functions that are implemented in topicmod.evaluate.
Each topic modeling sub-module defines two important sequences: AVAILABLE_METRICS and DEFAULT_METRICS. The former lists all available metrics for that sub-module, the latter lists the default metrics that are used when you don’t specify anything with the metric parameter. Let’s have a look at both sequences in topicmod.tm_lda:
[14]:
from tmtoolkit.topicmod import tm_lda
tm_lda.AVAILABLE_METRICS
[14]:
('loglikelihood',
'cao_juan_2009',
'arun_2010',
'coherence_mimno_2011',
'griffiths_2004',
'held_out_documents_wallach09',
'coherence_gensim_u_mass',
'coherence_gensim_c_v',
'coherence_gensim_c_uci',
'coherence_gensim_c_npmi')
[15]:
tm_lda.DEFAULT_METRICS
[15]:
('cao_juan_2009', 'coherence_mimno_2011')
For details about the metrics and the academic references, see the respective implementations in the topicmod.evaluate module.
We will now run the model evaluations with evaluate_topic_models using our previously generated list of varying hyperparameters var_params, some constant hyperparameters and the default set of metrics. We also set return_models=True which means to retain the generated models in the evaluation results. We can see, that we can also pass parameters to the model evaluation functions. Here, we set the top_n and include_prob
parameters for the metric_coherence_mimno_2011 evaluation function.
[16]:
from tmtoolkit.topicmod.tm_lda import evaluate_topic_models
from tmtoolkit.topicmod.evaluate import results_by_parameter
const_params = {
'n_iter': 1000,
'random_state': 20191122, # to make results reproducible
'eta': 0.1, # sometimes also called "beta"
}
eval_results = evaluate_topic_models(dtm_bg,
varying_parameters=var_params,
constant_parameters=const_params,
coherence_mimno_2011_top_n=10,
coherence_mimno_2011_include_prob=True,
return_models=True)
eval_results[:3] # only show first three models
[16]:
[({'n_topics': 20,
'alpha': 0.05,
'n_iter': 1000,
'random_state': 20191122,
'eta': 0.1},
{'model': <lda.lda.LDA at 0x7f8a54426080>,
'cao_juan_2009': 0.12552942076573556,
'coherence_mimno_2011': -382.6720144016515}),
({'n_topics': 40,
'alpha': 0.025,
'n_iter': 1000,
'random_state': 20191122,
'eta': 0.1},
{'model': <lda.lda.LDA at 0x7f8a0ad2f490>,
'cao_juan_2009': 0.12268842815551809,
'coherence_mimno_2011': -376.3829891678098}),
({'n_topics': 30,
'alpha': 0.03333333333333333,
'n_iter': 1000,
'random_state': 20191122,
'eta': 0.1},
{'model': <lda.lda.LDA at 0x7f8a0ad2f4f0>,
'cao_juan_2009': 0.12662815448219536,
'coherence_mimno_2011': -377.67258877441253})]
The evaluation results are a list with pairs of hyperparameters and their evaluation results for each metric. Additionally, there is the generated model for each hyperparameter set.
We now use results_by_parameter, which takes the “raw” evaluation results and sorts them by a specific hyperparameter, in this case n_topics. This is important because this is the way that the function for visualizing evaluation results, plot_eval_results, expects the input.
[17]:
eval_results_by_topics = results_by_parameter(eval_results, 'n_topics')
eval_results_by_topics[:3] # again only the first three models
[17]:
[(20,
{'model': <lda.lda.LDA at 0x7f8a54426080>,
'cao_juan_2009': 0.12552942076573556,
'coherence_mimno_2011': -382.6720144016515}),
(30,
{'model': <lda.lda.LDA at 0x7f8a0ad2f4f0>,
'cao_juan_2009': 0.12662815448219536,
'coherence_mimno_2011': -377.67258877441253}),
(40,
{'model': <lda.lda.LDA at 0x7f8a0ad2f490>,
'cao_juan_2009': 0.12268842815551809,
'coherence_mimno_2011': -376.3829891678098})]
We can now see the results for each metric across the specified range of number of topics using plot_eval_results:
[18]:
from tmtoolkit.topicmod.visualize import plot_eval_results
plot_eval_results(eval_results_by_topics);
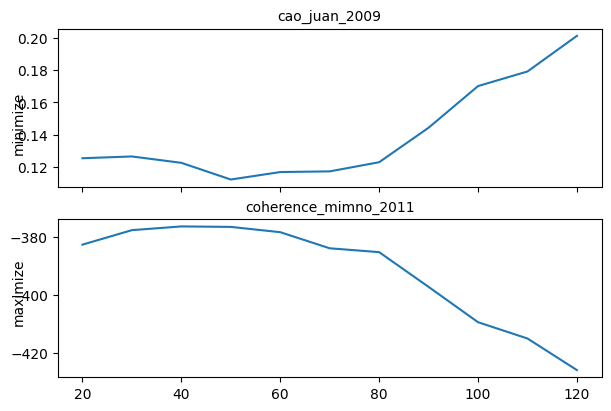
The evaluation metrics seem to agree and show best fits for models with 30 to 70 topics. We would normally investigate a set of models in this range, but for simplicity, lets continue with a model with n_topics=50 and alpha=0.02. We don’t have to generate a model with these hyperparameters again, because it’s already in the evaluation results (thanks to return_models=True). We extract the model from there in order to use it in the rest of the chapter.
[19]:
best_tm = [m for k, m in eval_results_by_topics if k == 50][0]['model']
best_tm.n_topics, best_tm.alpha, best_tm.eta # just to make sure
[19]:
(50, 0.02, 0.1)
Common statistics and tools for topic models
The topicmod.model_stats module mostly contains functions that compute statistics from the document-topic and topic-word distribution of a topic model and also some helper functions for working with such distributions. We’ll start with an important helper function, generate_topic_labels_from_top_words.
Generating labels for topics
In topic modeling, topics are numbered because they’re abstract – they’re simply a probability distribution across all words in the vocabulary. Still, it’s useful to give them labels for better identification. The function generate_topic_labels_from_top_words is very useful for that, as it finds labels according to the most “relevant” words in each topic. We’ll later see how we can identify the most relevant
words per topic using a special relevance statistic. Note that you can adjust the weight of the relevance measure for the ranking by using the parameter lambda_ which is in range \([0, 1]\).
The function requires at least the topic-word and document-topic distributions from the model, the document lengths and the vocabulary. It then finds the minimum number of relevant words that uniquely label each topic. You can also use a fixed number for that minimum number with the parameter n_words.
[20]:
from tmtoolkit.bow.bow_stats import doc_lengths
from tmtoolkit.topicmod.model_stats import generate_topic_labels_from_top_words
vocab_bg = np.array(vocab_bg) # we need this to be an array
doc_lengths_bg = doc_lengths(dtm_bg)
topic_labels = generate_topic_labels_from_top_words(
best_tm.topic_word_,
best_tm.doc_topic_,
doc_lengths_bg,
np.array(vocab_bg),
lambda_=0.6
)
topic_labels[:10] # showing only the first 5 topics here
[20]:
array(['1_justice_charge', '2_north_post', '3_error_night',
'4_sanction_action', '5_play_win', '6_say_issue', '7_shoot_police',
'8_attack_group', '9_hope_family', '10_morning_day'], dtype='<U23')
As we can see, two words are necessary to label each topic uniquely. By default, each label is prefixed with a number. You can change that with the parameter labels_format.
Let’s have a look at the top words for a specific topic. We can use ldamodel_top_topic_words for that from the module topicmod.model_io, which we will have a closer look at later:
[21]:
from tmtoolkit.topicmod.model_io import ldamodel_top_topic_words
top_topic_word = ldamodel_top_topic_words(best_tm.topic_word_,
vocab_bg,
row_labels=topic_labels)
top_topic_word[top_topic_word.index == '7_shoot_police']
[21]:
| rank_1 | rank_2 | rank_3 | rank_4 | rank_5 | rank_6 | rank_7 | rank_8 | rank_9 | rank_10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| topic | ||||||||||
| 7_shoot_police | say (0.06056) | police (0.05721) | shoot (0.03714) | man (0.0271) | morning (0.0271) | individual (0.02375) | operation (0.01706) | office (0.01706) | press (0.01706) | officer (0.01706) |
Marginal topic and word distributions
We’ll now focus on the marginal topic and word distributions. Let’s get the marginal topic distribution first by using marginal_topic_distrib:
[22]:
from tmtoolkit.topicmod.model_stats import marginal_topic_distrib
marg_topic = marginal_topic_distrib(best_tm.doc_topic_, doc_lengths_bg)
marg_topic
[22]:
array([0.01326, 0.0101 , 0.01326, 0.01243, 0.01669, 0.03903, 0.01335,
0.02143, 0.01505, 0.01166, 0.02023, 0.00638, 0.01657, 0.02442,
0.01864, 0.01632, 0.0353 , 0.01557, 0.02558, 0.03151, 0.07525,
0.03137, 0.03799, 0.01722, 0.03849, 0.01601, 0.01176, 0.02722,
0.01473, 0.01371, 0.01834, 0.02296, 0.01685, 0.01186, 0.01732,
0.01836, 0.00658, 0.00946, 0.02799, 0.01426, 0.02066, 0.01451,
0.02185, 0.01681, 0.01152, 0.02701, 0.02122, 0.00784, 0.0203 ,
0.01379])
The marginal topic distribution can be interpreted as the “importance” of each topic for the whole corpus. Let’s get the sorted indices into topic_labels with np.argsort and get the top five topics:
[23]:
# np.argsort gives ascending order, hence reverse via [::-1]
topic_labels[np.argsort(marg_topic)[::-1][:5]]
[23]:
array(['21_year_time', '6_say_issue', '25_america_american',
'23_white_trump', '17_country_love'], dtype='<U23')
Likewise, we can get the marginal word distribution with marginal_word_distrib from the model’s topic-word distribution and the marginal topic distribution. We’ll use this to list the most probable words for the corpus. As expected, these are mostly quite common words:
[24]:
from tmtoolkit.topicmod.model_stats import marginal_word_distrib
marg_word = marginal_word_distrib(best_tm.topic_word_, marg_topic)
vocab_bg[np.argsort(marg_word)[::-1][:10]]
[24]:
array(['say', 'year', 'people', 'country', 'new', 'time', 'trump',
'report', 'china', 'president'], dtype='<U14')
Two helper functions exist for this purpose: most_probable_words and least_probable_words sort the vocabulary according to the marginal probability:
[25]:
from tmtoolkit.topicmod.model_stats import most_probable_words, least_probable_words
most_probable_words(vocab_bg, best_tm.topic_word_,
best_tm.doc_topic_, doc_lengths_bg,
n=10)
[25]:
array(['say', 'year', 'people', 'country', 'new', 'time', 'trump',
'report', 'china', 'president'], dtype='<U14')
[26]:
least_probable_words(vocab_bg, best_tm.topic_word_,
best_tm.doc_topic_, doc_lengths_bg,
n=10)
[26]:
array(['urge', 'reveal', 'conduct', 'indicate', 'seven', 'controversial',
'analysis', 'argue', 'associate', 'guarantee'], dtype='<U14')
Word distinctiveness and saliency
Word distinctiveness and saliency (see below) help to identify the most “informative” words in a corpus given its topic model. Both measures are introduced in Chuang et al. 2012.
Word distinctiveness is calculated for each word \(w\) as
\(\text{distinctiveness}(w) = \sum_T(P(T|w) \log \frac{P(T|w)}{P(T)})\).
where \(P(T)\) is the marginal topic distribution and \(P(T|w)\) is the probability of a topic given a word \(w\).
We can calculate this measure using word_distinctiveness. To use this measure directly to rank words, we can use most_distinct_words and least_distinct_words:
[27]:
from tmtoolkit.topicmod.model_stats import word_distinctiveness, \
most_distinct_words, least_distinct_words
word_distinct = word_distinctiveness(best_tm.topic_word_, marg_topic)
word_distinct[:10] # first 10 words in vocab
[27]:
array([0.78729, 1.72026, 1.02646, 1.08976, 1.46623, 0.75563, 0.9307 ,
0.79992, 1.37157, 1.40561])
[28]:
most_distinct_words(vocab_bg, best_tm.topic_word_,
best_tm.doc_topic_, doc_lengths_bg,
n=10)
[28]:
array(['north', 'bank', 'flight', 'china', 'space', 'judge', 'justice',
'display', 'relation', 'morning'], dtype='<U14')
[29]:
least_distinct_words(vocab_bg, best_tm.topic_word_,
best_tm.doc_topic_, doc_lengths_bg,
n=10)
[29]:
array(['rely', 'series', 'ready', 'discussion', 'saturday', 'adopt',
'ago', 'well', 'sure', 'away'], dtype='<U14')
Word saliency weights each words’ distinctiveness by it’s marginal probability \(P(w)\):
\(\text{saliency}(w) = P(w) \cdot \text{distinctiveness}(w)\).
The respective functions in tmtoolkit are word_saliency, most_salient_words and least_salient_words:
[30]:
from tmtoolkit.topicmod.model_stats import word_saliency, \
most_salient_words, least_salient_words
word_sal = word_saliency(best_tm.topic_word_, best_tm.doc_topic_, doc_lengths_bg)
word_sal[:10] # first 10 words in vocab
[30]:
array([0.00079, 0.00182, 0.0008 , 0.00085, 0.00081, 0.00061, 0.00065,
0.00048, 0.00095, 0.00098])
[31]:
most_salient_words(vocab_bg, best_tm.topic_word_,
best_tm.doc_topic_, doc_lengths_bg,
n=10)
[31]:
array(['say', 'china', 'trump', 'year', 'country', 'people', 'report',
'president', 'new', 'company'], dtype='<U14')
[32]:
least_salient_words(vocab_bg, best_tm.topic_word_,
best_tm.doc_topic_, doc_lengths_bg,
n=10)
[32]:
array(['series', 'rely', 'discussion', 'adopt', 'ready', 'avoid', 'sure',
'saturday', 'theme', 'reportedly'], dtype='<U14')
Topic-word relevance
The topic-word relevance measure as introduced by Sievert and Shirley 2014 helps to identify the most relevant words within a topic by also accounting for the marginal probability of each word across the corpus. This is done by integrating a lift value, which is the “ratio of a term’s probability within a topic to its marginal probability across the corpus.” (ibid.)
Thus for each word \(w\), given a topic-word distribution \(\phi\), a topic \(t\) and a weight parameter \(\lambda\), it is calculated as:
\(\text{relevance}_{\phi, \lambda}(w, t) = \lambda \log \phi_{t,w} + (1-\lambda) \log \frac{\phi_{t,w}}{p(w)}\).
The first term \(\log \phi_{t,w}\) is the log of the topic-word distribution, the second term \(\log \frac{\phi_{t,w}}{p(w)}\) is the log lift and \(\lambda\) can be used to control the weight between both terms. The lower \(\lambda\), the more weight is put on the lift term, i.e. the more different are the results from the original topic-word distribution.
This measure is implemented in topic_word_relevance. It returns a matrix of the same shape as the topic-word distribution, i.e. each row represents a topic with a (log-transformed) distribution across all words in the vocabulary. Please note that the lambda parameter ends with an underscore: lambda_.
[33]:
from tmtoolkit.topicmod.model_stats import topic_word_relevance
topic_word_rel = topic_word_relevance(best_tm.topic_word_, best_tm.doc_topic_,
doc_lengths_bg, lambda_=0.6)
topic_word_rel
[33]:
array([[-5.23465, -5.25598, -5.13452, ..., -6.14689, -5.22336, -5.40088],
[-5.04211, -5.06343, -4.94197, ..., -5.95435, -5.03081, -5.20834],
[-5.23465, -5.25598, -5.13452, ..., -6.14689, -5.22336, -5.40088],
...,
[-4.87349, -1.18125, -4.77336, ..., -3.38784, -4.8622 , -5.03972],
[-5.56688, -5.58821, -5.46674, ..., -1.96826, -5.55559, -5.73311],
[-5.26451, -5.28584, -5.16438, ..., -6.17675, -5.25322, -5.43074]])
To confirm that it’s 50 topics across all words in the vocabulary:
[34]:
topic_word_rel.shape
[34]:
(50, 789)
Two functions can be used to get the most or least relevant words for a topic: most_relevant_words_for_topic and least_relevant_words_for_topic. You can select the topic with the topic parameter which is a zero-based topic index.
We’ll do it for topic with index 9, which is:
[35]:
topic_labels[9]
[35]:
'10_morning_day'
[36]:
from tmtoolkit.topicmod.model_stats import most_relevant_words_for_topic, \
least_relevant_words_for_topic
most_relevant_words_for_topic(vocab_bg, topic_word_rel, topic=9, n=10)
[36]:
array(['morning', 'day', 'partner', 'start', 'walk', 'likely', 'chance',
'help', 'foot', 'boost'], dtype='<U14')
[37]:
least_relevant_words_for_topic(vocab_bg, topic_word_rel, topic=9, n=10)
[37]:
array(['say', 'year', 'people', 'country', 'new', 'time', 'trump',
'report', 'china', 'president'], dtype='<U14')
Topic coherence
We already used the coherence metric (Mimno et al. 2011) for topic model evaluation. However, this metric cannot only be used to assess the overall quality of a topic model, but also to evaluate the individual topics’ coherence.
[38]:
from tmtoolkit.topicmod.evaluate import metric_coherence_mimno_2011
# use top 20 words per topic for metric
coh = metric_coherence_mimno_2011(best_tm.topic_word_, dtm_bg, top_n=10, include_prob=True)
coh
[38]:
array([-381.19764, -405.21699, -385.14085, -382.9605 , -377.73554,
-385.5327 , -381.7741 , -366.53703, -384.22751, -387.94505,
-374.08057, -377.80028, -369.7097 , -368.60895, -393.62278,
-402.06989, -356.06615, -373.96911, -339.94301, -350.93052,
-345.55067, -349.02383, -350.14311, -365.86664, -373.2819 ,
-368.1276 , -399.61229, -371.58258, -381.01624, -407.47346,
-376.48966, -390.12855, -405.42291, -387.12314, -361.73032,
-372.84445, -393.99511, -380.1421 , -370.90795, -367.79897,
-381.71496, -373.34488, -358.05694, -366.27945, -367.27849,
-389.31761, -368.70005, -406.87429, -381.88397, -370.53712])
This generates a coherence value for each topic. Let’s show the distribution of these values:
[39]:
import matplotlib.pyplot as plt
plt.hist(coh, bins=20)
plt.xlabel('coherence')
plt.ylabel('n')
plt.show();
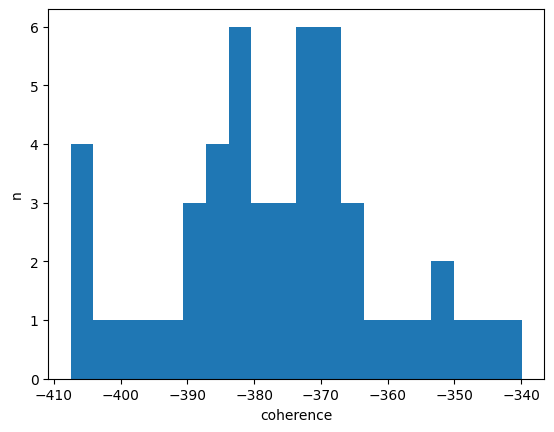
And print the best and worst topics according to this metric:
[40]:
import numpy as np
top10_t_indices = np.argsort(coh)[::-1][:10]
bottom10_t_indices = np.argsort(coh)[:10]
topic_labels[top10_t_indices]
[40]:
array(['19_al_syrian', '21_year_time', '22_china_chinese',
'23_white_trump', '20_report_agency', '17_country_love',
'43_russian_moscow', '35_intelligence_russia', '24_parent_child',
'44_bill_health'], dtype='<U23')
[41]:
topic_labels[bottom10_t_indices]
[41]:
array(['30_step_authority', '48_bank_asset', '33_force_group',
'2_north_post', '16_2011_people', '27_space_european',
'37_relation_contact', '15_club_institute', '32_fight_provide',
'46_say_mr'], dtype='<U23')
Note that this metric also doesn’t spare oneself careful manual evaluation, because it can also be off for some topics. For example, topic 21_year_time is certainly not a coherent topic as it mostly ranks very common but less meaningful words high:
[42]:
top_topic_word[top_topic_word.index == '21_year_time']
[42]:
| rank_1 | rank_2 | rank_3 | rank_4 | rank_5 | rank_6 | rank_7 | rank_8 | rank_9 | rank_10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| topic | ||||||||||
| 21_year_time | say (0.08178) | year (0.06211) | time (0.04395) | people (0.03639) | come (0.02428) | want (0.02201) | tell (0.02126) | work (0.01974) | go (0.01899) | long (0.01823) |
More coherence metrics can be used with the function metric_coherence_gensim. This requires that gensim is installed. Furthemore, most metrics require that a parameter texts is passed which is the tokenized text that was used to create the document-term matrix.
Filtering topics
With the function filter_topics, you can filter the topics according to their topic-word distribution and the following search criteria:
search_pattern: one or more search patterns according to the common parameters for pattern matchingtop_n: pattern match(es) must occur in the firsttop_nmost probable words in the topicthresh: matched words’ probability must be above this threshold
You must specify at least one of top_n and thresh, but you can also specify both. The function returns an array of topic indices (which start with zero!).
Let’s find all topics that have the glob pattern (match_type='glob') “russ*” (to match both “russia” and “russian”) in the top 5 most probable words:
[43]:
from tmtoolkit.topicmod.model_stats import filter_topics
found_topics = filter_topics('russ*', vocab_bg,
best_tm.topic_word_, match_type='glob',
top_n=5)
found_topics
[43]:
array([ 3, 34, 42])
We can use these indices with our topic_labels:
[44]:
topic_labels[found_topics]
[44]:
array(['4_sanction_action', '35_intelligence_russia', '43_russian_moscow'],
dtype='<U23')
Next, we want to select all topics where any of the words matched by the glob patterns "chin*" or "business" achieve at least a probability of 0.01 (thresh=0.01):
[45]:
found_topics = filter_topics(['chin*', 'business'], vocab_bg,
best_tm.topic_word_, thresh=0.01, match_type='glob')
topic_labels[found_topics]
[45]:
array(['6_say_issue', '9_hope_family', '22_china_chinese',
'27_space_european'], dtype='<U23')
When we specify cond='all', all patterns must have at least one match (here in the top 10 list of words per topic):
[46]:
found_topics = filter_topics(['chin*', 'business'], vocab_bg,
best_tm.topic_word_, top_n=10, match_type='glob',
cond='all')
topic_labels[found_topics] # no result
[46]:
array([], dtype='<U23')
You could also pass a topic-word relevance matrix instead of a topic-word probability distribution.
[47]:
found_topics = filter_topics('russ*', vocab_bg,
topic_word_rel, match_type='glob',
top_n=5)
topic_labels[found_topics]
[47]:
array(['4_sanction_action', '35_intelligence_russia', '43_russian_moscow'],
dtype='<U23')
Excluding topics
It is often the case that some topics of a topic model rank a lot of uninformative (e.g. very common) words the highest. This results in some uninformative topics, which you may want to exclude from further analysis. Note that if a large fraction of topics seems uninformative, it points to a problem with your topic model and/or your preprocessing steps. You should evaluate your candidate models carefully with the mentioned metrics and/or adjust your text preprocessing pipeline.
The function exclude_topics allows to remove a specified set of topics from the document-topic and topic-word distributions. You need to pass the zero-based indices of the topics that you want to remove, and both distributions.
For example, suppose the following topics were identified as uninformative:
[48]:
uninform_topics = [5, 20, 32, 40, 45]
topic_labels[uninform_topics]
[48]:
array(['6_say_issue', '21_year_time', '33_force_group', '41_line_look',
'46_say_mr'], dtype='<U23')
We can now pass these indices to exclude_topics along with the topic model distributions. We’ll get back new, filtered, distributions.
[49]:
from tmtoolkit.topicmod.model_stats import exclude_topics
new_doc_topic, new_topic_word, new_topic_mapping = \
exclude_topics(uninform_topics, best_tm.doc_topic_,
best_tm.topic_word_, return_new_topic_mapping=True)
new_doc_topic.shape, new_topic_word.shape
[49]:
((100, 45), (45, 789))
We can see in the new distributions’ shapes that we now have 47 instead of 50 topics, because we removed three of them. We shouldn’t forget to also update the topic labels and remove the unwanted topics:
[50]:
new_topic_labels = np.delete(topic_labels, uninform_topics)
new_topic_labels
[50]:
array(['1_justice_charge', '2_north_post', '3_error_night',
'4_sanction_action', '5_play_win', '7_shoot_police',
'8_attack_group', '9_hope_family', '10_morning_day',
'11_german_germany', '12_council_circumstance',
'13_southern_reject', '14_investment_company', '15_club_institute',
'16_2011_people', '17_country_love', '18_officer_police',
'19_al_syrian', '20_report_agency', '22_china_chinese',
'23_white_trump', '24_parent_child', '25_america_american',
'26_world_meeting', '27_space_european', '28_company_reform',
'29_fire_death', '30_step_authority', '31_party_leader',
'32_fight_provide', '34_percent_french', '35_intelligence_russia',
'36_trump_president', '37_relation_contact', '38_flight_display',
'39_vote_feel', '40_election_northern', '42_man_accord',
'43_russian_moscow', '44_bill_health', '45_judge_victim',
'47_minister_president', '48_bank_asset', '49_mr_damage',
'50_note_sell'], dtype='<U23')
Displaying and exporting topic modeling results
The topicmod.model_io module provides several functions for displaying and exporting topic modeling results, i.e. results derived from the document-topic and topic-word distribution of a given topic model.
We already used ldamodel_top_topic_words briefly, which generates a dataframe with the top words from a topic-word distribution. You can also use the topic-word relevance matrix instead. With top_n we can control the number of top words:
[51]:
# using relevance matrix here and showing only the first 3 topics
ldamodel_top_topic_words(topic_word_rel, vocab_bg, top_n=5)[:3]
[51]:
| rank_1 | rank_2 | rank_3 | rank_4 | rank_5 | |
|---|---|---|---|---|---|
| topic | |||||
| topic_1 | justice (-0.2563) | charge (-0.6977) | department (-0.7619) | need (-0.9191) | future (-1.037) |
| topic_2 | north (0.3636) | post (-0.7892) | leader (-0.8919) | body (-0.916) | tie (-1.246) |
| topic_3 | error (-0.7178) | night (-0.8708) | stage (-0.8802) | hand (-1.057) | case (-1.08) |
If you’re interested in the top topics for each word/token, you can use ldamodel_top_word_topics. Here, we generate the top five topics for each token in the vocabulary, but only display the output for four specific words. Instead of the generic "topic_..." topic names, we additionally pass our previously generated topic labels topic_labels:
[52]:
from tmtoolkit.topicmod.model_io import ldamodel_top_word_topics
top_word_topics = ldamodel_top_word_topics(topic_word_rel, vocab_bg,
top_n=5, topic_labels=topic_labels)
top_word_topics[top_word_topics.index.isin(['china', 'chinese', 'russia', 'russian'])]
[52]:
| rank_1 | rank_2 | rank_3 | rank_4 | rank_5 | |
|---|---|---|---|---|---|
| token | |||||
| china | 22_china_chinese (0.2341) | 14_investment_company (-3.969) | 12_council_circumstance (-5.398) | 37_relation_contact (-5.414) | 48_bank_asset (-5.521) |
| chinese | 22_china_chinese (-0.617) | 27_space_european (-1.682) | 5_play_win (-2.617) | 12_council_circumstance (-4.999) | 37_relation_contact (-5.015) |
| russia | 43_russian_moscow (-0.6884) | 35_intelligence_russia (-0.7184) | 4_sanction_action (-1.154) | 5_play_win (-2.73) | 9_hope_family (-3.295) |
| russian | 43_russian_moscow (-0.08055) | 35_intelligence_russia (-1.267) | 19_al_syrian (-2.768) | 29_fire_death (-3.359) | 5_play_win (-3.46) |
Note that the values in parantheses are the corresponding values from the matrix for that word in that topic. They’re negative because of the log transformation that is applied in the topic-word relevance measure.
Similar functions can be used for the document-topic distribution: ldamodel_top_doc_topics gives the top topics per document and ldamodel_top_topic_docs gives the top documents per topic. Here, top_n controls the number of top-ranked topics or documents to return, respectively. This time, we use the filtered document-topic distribution new_doc_topics:
[53]:
from tmtoolkit.topicmod.model_io import ldamodel_top_doc_topics
ldamodel_top_doc_topics(new_doc_topic, doc_labels_bg, top_n=3,
topic_labels=new_topic_labels)[:5]
[53]:
| rank_1 | rank_2 | rank_3 | |
|---|---|---|---|
| document | |||
| NewsArticles-1032 | 31_party_leader (0.9579) | 20_report_agency (0.01743) | 39_vote_feel (0.01743) |
| NewsArticles-1036 | 8_attack_group (0.2678) | 20_report_agency (0.2302) | 11_german_germany (0.1927) |
| NewsArticles-104 | 49_mr_damage (0.5089) | 9_hope_family (0.2557) | 47_minister_president (0.1291) |
| NewsArticles-1043 | 5_play_win (0.5088) | 19_al_syrian (0.2622) | 7_shoot_police (0.2006) |
| NewsArticles-1048 | 18_officer_police (0.7435) | 20_report_agency (0.1931) | 4_sanction_action (0.04303) |
And now for the top documents per topic:
[54]:
from tmtoolkit.topicmod.model_io import ldamodel_top_topic_docs
ldamodel_top_topic_docs(new_doc_topic, doc_labels_bg, top_n=3,
topic_labels=new_topic_labels)[:5]
[54]:
| rank_1 | rank_2 | rank_3 | |
|---|---|---|---|
| topic | |||
| 1_justice_charge | NewsArticles-1341 (0.8213) | NewsArticles-2617 (0.4118) | NewsArticles-248 (0.1688) |
| 2_north_post | NewsArticles-2101 (0.6114) | NewsArticles-3573 (0.5619) | NewsArticles-3023 (0.4452) |
| 3_error_night | NewsArticles-1539 (0.8661) | NewsArticles-1295 (0.7066) | NewsArticles-1090 (0.6058) |
| 4_sanction_action | NewsArticles-709 (0.5343) | NewsArticles-3246 (0.4311) | NewsArticles-3263 (0.2096) |
| 5_play_win | NewsArticles-693 (0.9697) | NewsArticles-1126 (0.604) | NewsArticles-3263 (0.5384) |
There are also two functions that generate datatables for the full topic-word and document-topic distributions: ldamodel_full_topic_words and ldamodel_full_doc_topics. The output of both functions is naturally quite big, as long as you’re not working with a “toy dataset”.
[55]:
from tmtoolkit.topicmod.model_io import ldamodel_full_topic_words
df_topic_word = ldamodel_full_topic_words(new_topic_word,
vocab_bg,
row_labels=new_topic_labels)
# displaying only the first 5 topics with 10 tokens
# from sorted vocabulary list (tokens 120 to 129)
df_topic_word.iloc[:5, 120:130]
[55]:
| central | centre | century | certain | chairman | challenge | chance | change | charge | check | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.000337 | 0.000337 | 0.000337 | 0.000337 | 0.000337 | 0.003705 | 0.003705 | 0.000337 | 0.034018 | 0.000337 |
| 1 | 0.000408 | 0.000408 | 0.000408 | 0.000408 | 0.000408 | 0.000408 | 0.000408 | 0.000408 | 0.000408 | 0.008575 |
| 2 | 0.000337 | 0.000337 | 0.000337 | 0.000337 | 0.000337 | 0.000337 | 0.000337 | 0.000337 | 0.003705 | 0.000337 |
| 3 | 0.000353 | 0.000353 | 0.000353 | 0.000353 | 0.000353 | 0.000353 | 0.000353 | 0.000353 | 0.000353 | 0.000353 |
| 4 | 0.000282 | 0.000282 | 0.003099 | 0.000282 | 0.000282 | 0.000282 | 0.000282 | 0.003099 | 0.000282 | 0.000282 |
[56]:
from tmtoolkit.topicmod.model_io import ldamodel_full_doc_topics
df_doc_topic = ldamodel_full_doc_topics(new_doc_topic,
doc_labels_bg,
topic_labels=new_topic_labels)
# displaying only the first 3 documents with the first
# 5 topics
df_doc_topic.iloc[:3, :5]
[56]:
| _doc | 1_justice_charge | 2_north_post | 3_error_night | 4_sanction_action | |
|---|---|---|---|---|---|
| 0 | NewsArticles-1032 | 0.000173 | 0.000173 | 0.000173 | 0.000173 |
| 1 | NewsArticles-1036 | 0.000094 | 0.000094 | 0.000094 | 0.000094 |
| 2 | NewsArticles-104 | 0.002532 | 0.002532 | 0.002532 | 0.002532 |
For quick inspection of topics there’s also a pair of print functions. We already used print_ldamodel_topic_words, but we haven’t tried print_ldamodel_doc_topics yet. This prints the top_n most probable topics for each document:
[57]:
from tmtoolkit.topicmod.model_io import print_ldamodel_doc_topics
# subsetting new_doc_topic and doc_labels to get only the first
# five documents
print_ldamodel_doc_topics(new_doc_topic[:5, :], doc_labels_bg[:5],
val_labels=new_topic_labels)
NewsArticles-1032
> #1. 31_party_leader (0.957895)
> #2. 20_report_agency (0.017429)
> #3. 39_vote_feel (0.017429)
NewsArticles-1036
> #1. 8_attack_group (0.267825)
> #2. 20_report_agency (0.230249)
> #3. 11_german_germany (0.192673)
NewsArticles-104
> #1. 49_mr_damage (0.508861)
> #2. 9_hope_family (0.255696)
> #3. 47_minister_president (0.129114)
NewsArticles-1043
> #1. 5_play_win (0.508783)
> #2. 19_al_syrian (0.262250)
> #3. 7_shoot_police (0.200616)
NewsArticles-1048
> #1. 18_officer_police (0.743531)
> #2. 20_report_agency (0.193138)
> #3. 4_sanction_action (0.043031)
You can also export the results of a topic model to an Excel file using save_ldamodel_summary_to_excel. The resulting Excel file will contain the following sheets:
top_doc_topics_vals: document-topic distribution with probabilities of top topics per documenttop_doc_topics_labels: document-topic distribution with labels of top topics per documenttop_doc_topics_labelled_vals: document-topic distribution combining probabilities and labels of top topics per document (e.g."topic_12 (0.21)")top_topic_word_vals: topic-word distribution with probabilities of top words per topictop_topic_word_labels: topic-word distribution with top words per (e.g."politics") topictop_topic_words_labelled_vals: topic-word distribution combining probabilities and top words per topic (e.g."politics (0.08)")optional if
dtmis given –marginal_topic_distrib: marginal topic distribution
Additionally to saving the output to the specified Excel file, the function will also return a dict with the sheets and their data.
[58]:
from tmtoolkit.topicmod.model_io import save_ldamodel_summary_to_excel
sheets = save_ldamodel_summary_to_excel('data/news_articles_100.xlsx',
new_topic_word, new_doc_topic,
doc_labels_bg, vocab_bg,
dtm = dtm_bg,
topic_labels = new_topic_labels)
To quickly store a topic model to disk for sharing or loading again at a later point in time, there are save_ldamodel_to_pickle and load_ldamodel_from_pickle. The function for saving takes a path to a pickle file to create (or update), a topic model object (such as an LDA instance as best_tm, but you could also pass a tuple like
(new_doc_topic, new_topic_word)), the corresponding vocabulary and document labels, and optionally the DTM that was used to create the topic model. The function for loading the data will return the saved data as a dict. We will only show the dict’s keys here, as the data itself is too large to be printed:
[59]:
from tmtoolkit.topicmod.model_io import save_ldamodel_to_pickle, \
load_ldamodel_from_pickle
save_ldamodel_to_pickle('data/news_articles_100.pickle',
best_tm, vocab_bg, doc_labels_bg,
dtm = dtm_bg)
loaded = load_ldamodel_from_pickle('data/news_articles_100.pickle')
loaded.keys()
[59]:
dict_keys(['model', 'vocab', 'doc_labels', 'dtm'])
Visualizing topic models
The topicmod.visualize module contains several functions to visualize topic models and evaluation results. We’ve already used plot_eval_results during topic model evaluation so we’ll now focus on visualizing topic models.
Heatmaps
Let’s start with heatmap visualizations of document-topic or topic-word distributions from our topic model. This can be done with plot_doc_topic_heatmap and plot_topic_word_heatmap respectively. Both functions draw on a matplotlib figure and Axes object, which you must create before using these functions.
Heatmap visualizations essentially shade cells in a 2D matrix (like the document-topic or topic-word distributions) according to their value, i.e. the respective probability for a topic in a given document or a word in a given topic. Since these matrices are usually quite large, i.e. with hundreds of rows and/or columns, it doesn’t make sense to plot a heatmap of the whole matrix, but rather a certain subset of interest. When we want to visualize a document-topic distribution, we can optionally
select a subset of the documents with the which_documents parameter and a subset of the topics with the which_topics parameter. Let’s draw a heatmap of a subset of documents across all topics at first:
[60]:
import matplotlib.pyplot as plt
from tmtoolkit.topicmod.visualize import plot_doc_topic_heatmap
# create a figure of certain size and
# Axes object to draw on
fig, ax = plt.subplots(figsize=(32, 8))
# randomly selecting a subset of documents
which_docs = random.sample(doc_labels_bg, 5)
plot_doc_topic_heatmap(fig, ax, new_doc_topic, doc_labels_bg,
topic_labels=new_topic_labels,
which_documents=which_docs);

[61]:
fig, ax = plt.subplots(figsize=(6, 8))
# randomly selecting a subset of topics
which_topics = random.sample(list(new_topic_labels), 10)
plot_doc_topic_heatmap(fig, ax, new_doc_topic, doc_labels_bg,
topic_labels=new_topic_labels,
which_documents=which_docs,
which_topics=which_topics);
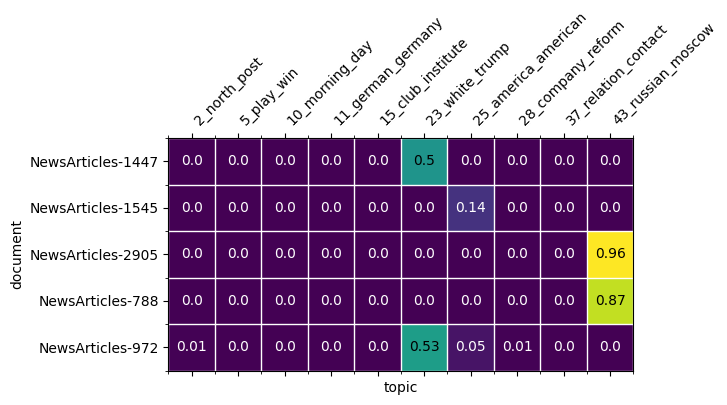
Similarily, we can work with plot_topic_word_heatmap to visualize a topic-word distribution. We can also select a subset of topics and words from the vocabulary:
[62]:
from tmtoolkit.topicmod.visualize import plot_topic_word_heatmap
fig, ax = plt.subplots(figsize=(12, 8))
which_words = ['trump', 'america', 'russia', 'germany']
plot_topic_word_heatmap(fig, ax, new_topic_word, vocab_bg,
topic_labels=new_topic_labels,
which_topics=which_topics,
which_words=which_words);
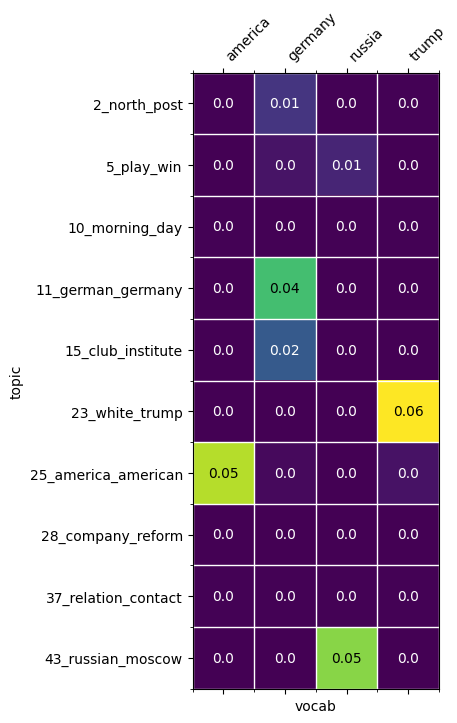
Note that there’s also a generic heatmap plotting function plot_heatmap for any kind of 2D matrices.
Word clouds
Thanks to the wordlcloud package, topic-word and document-topic distributions can also be visualized as “word clouds” with tmtoolkit. The function generate_wordclouds_for_topic_words generates a word cloud for each topic by scaling a topic’s word by its probability (weight). You can choose to display only the top top_n words per topic. The result of this function will be a
dictionary mapping topic labels to the respective word cloud image.
[63]:
from tmtoolkit.topicmod.visualize import generate_wordclouds_for_topic_words
# some options for wordcloud output
img_w = 400 # image width
img_h = 300 # image height
topic_clouds = generate_wordclouds_for_topic_words(
new_topic_word, vocab_bg,
top_n=20, topic_labels=new_topic_labels,
width=img_w, height=img_h
)
# show all generated word clouds
topic_clouds.keys()
[63]:
dict_keys(['1_justice_charge', '2_north_post', '3_error_night', '4_sanction_action', '5_play_win', '7_shoot_police', '8_attack_group', '9_hope_family', '10_morning_day', '11_german_germany', '12_council_circumstance', '13_southern_reject', '14_investment_company', '15_club_institute', '16_2011_people', '17_country_love', '18_officer_police', '19_al_syrian', '20_report_agency', '22_china_chinese', '23_white_trump', '24_parent_child', '25_america_american', '26_world_meeting', '27_space_european', '28_company_reform', '29_fire_death', '30_step_authority', '31_party_leader', '32_fight_provide', '34_percent_french', '35_intelligence_russia', '36_trump_president', '37_relation_contact', '38_flight_display', '39_vote_feel', '40_election_northern', '42_man_accord', '43_russian_moscow', '44_bill_health', '45_judge_victim', '47_minister_president', '48_bank_asset', '49_mr_damage', '50_note_sell'])
Let’s select specific topics and display their word cloud:
[64]:
topic_clouds['7_shoot_police']
[64]:

The same can be done for the document-topic distribution using generate_wordclouds_for_document_topics. Here, a word cloud for each document will be generated that contains the top_n most probable topics for this document:
[65]:
from tmtoolkit.topicmod.visualize import generate_wordclouds_for_document_topics
doc_clouds = generate_wordclouds_for_document_topics(
new_doc_topic, doc_labels_bg, topic_labels=new_topic_labels,
top_n=5, width=img_w, height=img_h)
# show only the first 5 documents for
# which word clouds were generated
list(doc_clouds.keys())[:5]
[65]:
['NewsArticles-1032',
'NewsArticles-1036',
'NewsArticles-104',
'NewsArticles-1043',
'NewsArticles-1048']
To display a specific document’s topic word cloud:
[66]:
doc_clouds['NewsArticles-1032']
[66]:

We can write the generated images as PNG files to a folder on disk. Here, we store all word clouds in topic_clouds to 'data/tm_wordclouds/':
[67]:
from tmtoolkit.topicmod.visualize import write_wordclouds_to_folder
write_wordclouds_to_folder(topic_clouds, 'data/tm_wordclouds/')
Interactive visualization with pyLDAVis
The pyLDAVis package offers a great interactive tool to explore a topic model. The tmtoolkit function parameters_for_ldavis allows to prepare your topic model data for this package so that you can easily pass it on to pyLDAVis.
[68]:
from tmtoolkit.topicmod.visualize import parameters_for_ldavis
ldavis_params = parameters_for_ldavis(new_topic_word,
new_doc_topic,
dtm_bg,
vocab_bg)
If you have installed the package, you can now start the LDAVis explorer with the following lines of code in a Jupyter notebook:
import pyLDAvis
pyLDAVis.prepare(**ldavis_params)